<< Click to Display Table of Contents >> RKP (Kenngrößen einer exponentiellen Regression)

Syntax:

RKP(y_Werte [; x_Werte] [; Konstante] [; Statistik])

Beschreibung:

Liefert verschiedene Kenngrößen einer exponentiellen Regression.

Unter einer exponentiellen Regression versteht man das Anpassen einer Exponentialkurve an eine Menge von Punkten (zum Beispiel den Messpunkten einer Messreihe).

Die Funktionsgleichung für diese Exponentialkurve lautet:

y = b*m^x

beziehungsweise (wenn mehrere Bereiche mit x-Werten vorliegen):

y = b * (m1^x1) * (m2^x2) * ... * (mn^xn)

RKP erwartet als Argumente die y-Werte (und, sofern angegeben, die zugehörigen x-Werte) und liefert als Ergebnis eine Matrix in der Form {mn . mn-1 . ... . m2 . m1 . b}.

Wird das optionale Argument Statistik verwendet, wird die resultierende Matrix um weitere Kenngrößen (Standardfehler, Bestimmtheitsmaß etc.) erweitert.

Die Funktion RKP erwartet folgende Argumente:

y_Werte: Hier geben Sie die vorliegenden y-Koordinaten, also die abhängigen Werte, an. y_Werte kann entweder ein Zellbezug oder eine Matrix sein.

x_Werte: Hier können optional die x-Koordinaten, also die unabhängigen Werte angegeben werden. Auch x_Werte kann entweder ein Zellbezug oder eine Matrix sein. Wird x_Werte nicht angegeben, verwendet die Funktion automatisch die Werte 1, 2, 3, ... (entsprechend der Anzahl der vorliegenden y_Werte).

Konstante: Mit dem optionalen Argument Konstante können Sie festlegen, ob die Konstante b auf Eins gesetzt werden soll:

WAHR oder nicht angegeben: b wird aus den vorliegenden Daten automatisch berechnet.

FALSCH: b wird fest auf Eins gesetzt, und die Kurve wird entsprechend "hingebogen". Dies geschieht durch Anpassen des Koeffizienten m.

Statistik: Das optionale Argument Statistik bestimmt, ob zusätzliche Kenngrößen geliefert werden sollen:

FALSCH oder nicht angegeben: keine zusätzlichen Kenngrößen liefern.

WAHR: zusätzliche Kenngrößen liefern. In diesem Falle wird eine Matrix zurückgeliefert, die nicht nur m und b, sondern folgende Werte enthält:

{mn . mn-1 . ... . m2 . m1 . b ; smn . smn-1 . ... . sm2 . sm1 . sb ; R2 . sey ; F. df ; ssreg . ssresid}

Grafisch dargestellt sieht diese Matrix also wie folgt aus:

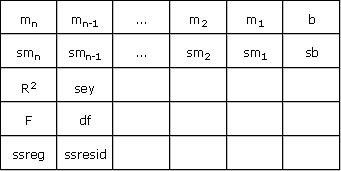
Bei obigen Kürzeln handelt es sich um folgende Kenngrößen:

Hinweis:

Diese Formel muss als Matrixformel eingegeben werden. Informationen dazu finden Sie im Abschnitt Arbeiten mit Matrizen.

Siehe auch:

RGP, TREND, VARIATION